
결정트리가 데이터를 split하는 기본 원리는 '균일도'를 기본으로 함.
'균일도' 또는 '혼잡도'를 나타내기 위해 사용하는 지표들 중
(1) 엔트로피 (entropy) 과 (2) 지니계수 (gini index)에 대해 다뤄보겠다.
내가 decision tree를 구현하기 위해서 사용하고 있는 scikit-learn에서는 CART 알고리즘을 이용하고,
CART 알고리즘은 지니계수를 이용하여 데이터를 split함.
Tree Algorithms : ID3, C4.5, C5.0, CART
ID3 : creates a multiway tree, finding for each node (i.e. in a greedy manner) the categorical feature that will yield the largest information gain for categorical targets. Trees are grown to their maximum size and then a pruning step is usually applied to improve the ability of the tree to generalize to unseen data.
C4.5 : ID3 개선 version, removed the restriction that features must be categorical by dynamically defining a discrete attribute (based on numerical variables) that partitions the continuous attribute value into a discrete set of intervals. C4.5 converts the trained trees (i.e. the output of the ID3 algorithm) into sets of if-then rules. The accuracy of each rule is then evaluated to determine the order in which they should be applied. Pruning is done by removing a rule’s precondition if the accuracy of the rule improves without it.
C5.0 : Quinlan’s latest version release under a proprietary license. It uses less memory and builds smaller rulesets than C4.5 while being more accurate.
CART (Classification and Regression Trees) : very similar to C4.5, but it differs in that it supports numerical target variables (regression) and does not compute rule sets. CART constructs binary trees using the feature and threshold that yield the largest information gain at each node.
출처 : https://scikit-learn.org/stable/modules/tree.html#tree-algorithms-id3-c4-5-c5-0-and-cart
엔트로피
- 엔트로피 Entropy ?
정보를 표현하는데 필요한 최소 평균 자원량 (정보량의 기댓값)
- 정보량 Intrinsic Value ?
어떤 사건을 표현하는 데 필요한 최소 자원량
- 다시 엔트로피로 돌아가보면,

엔트로피가 작을수록 분류가 잘 되어 있는 상태를 의미
그렇다면 ID3 알고리즘이 계산하는 information gain이 엔트로피를 어떻게 이용하는지 알아보자.
여기서 정보이득지수 (information gain ; IG)는 변수에 의해 데이터를 분할했을 때, 기대되는 엔트로피의 감소 정도 (두 엔트로피의 차이)

이제 ID3 알고리즘은 cost function으로 cross entropy를 이용하며,
entropy를 기반으로 구한 information gain을 최대화 하는 방향으로 결정노드를 만들 것이다.
( 분할하고 엔트로피가 작아질수록 그 차이: IG가 커지니까 )
실제 decision tree 에 적용해보면
(1) 먼저 레이블에 대한 Root Node를 생성하고, 전 사건의 엔트로피 (H(S))를 계산한다.
(2) 이전 데이터에 대해 피처별로 데이터를 분류해서 IG 지수를 계산한다.
(3) IG 지수 계산값이 가장 큰 피처로 결정노드를 생성한다. (이 때, 엔트로피가 0이면 리프노드가 된다.)
지니계수
데이터의 통계적 분산 정도를 나타내며, 0~1 사이의 값으로 나타남.
지니계수가 높을수록 잘 분류되지 못한 것. (예를 들어 클래스 '0'과 '1'이 고르게 50개, 50개 있는 상태)
따라서 CART 알고리즘은 cost function으로 gini index를 이용하므로, gain information이 커지는,
즉 gini index가 낮아지는 방향으로 분류를 전개한다.
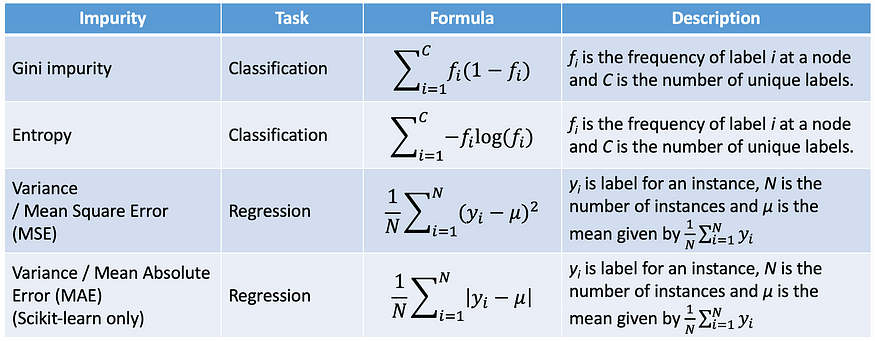
지니 불순도는 두 개의 데이터를 랜덤하게 골랐을 때 두 데이터의 클래스가 서로 다를 확률을 의미한다.
따라서 '어떤 클래스가 나올 확률' p_i에 '어떤 클래스가 나오지 않을 확률' 1-p_i를 곱한 것을 모두 더해주면 된다. (c는 클래스의 개수)

여기서도 엔트로피와 마찬가지로 정보이득(information gain)을 계산할 수 있을 것이고, 결국 정보이득을 최대화하는 방향으로 결정노드가 생성된다.
IG(S,V)의 계산방법에서 엔트로피를 그냥 Gini impurity로만 바꿔주면 동일하기 때문에 계산과정은 생략한다.
( 부모노드의 지니 불순도 - 왼쪽 노드 weight * 왼쪽 노드 지니 불순도 - 오른쪽 노드 weight * 오른쪽 노드 지니 불순도 )
'Study > 머신러닝' 카테고리의 다른 글
| 차원 축소 (0) | 2023.10.29 |
|---|---|
| 앙상블 학습 - Bagging (0) | 2023.09.25 |
| Decision Tree : 가지치기 (pruning)에 대하여 (1) | 2023.09.15 |
| Decision Tree : scikit learn의 feature_importances_는 어떻게 계산된 것일까? + Permutation Importance (1) | 2023.09.08 |
| PR Graph 성능 평가 (2) | 2023.09.07 |
