시계열 분해

 

시계열 패턴의 이해

 

- 3 요인 : 추세(trend) + 계절성(seasonality) + 주기성(cycle)

 

추세 : 데이터가 장기적으로 증가 또는 감소할 때 나타나는 패턴 

주기성 : 고정된 빈도가 아닌 형태로, 중기적으로 증가 또는 감소하는 모습을 보일 때 드러나는 패턴

계절성 :  1달, 1년 등 특정한 때에 단기로 나타나는 계절성 요인이 시계열 패턴에 영향을 줄 때 드러나는 패턴

 

+ 그 외 불규칙 요인 : 측정 및 예측이 어려운 오차에 의한 변동

 

 

---

성분을 분해할 수 있는 모형

 

크게 2가지 : 가법모형 & 승법모형 

 

[ 가법모형 ]

-  yt=St+Tt+Rt

-  yt가 원래 데이터, St가 계절 성분, Tt가 추세 - 주기 성분, Rt가 residual이다. 

 

[ 승법모형 ]

-  yt=St*Tt*Rt

-  log 변환하면 log(yt) = log(St) + log(Tt) + log(Rt) 로 변환 가능

-  시간의 흐름에 따라 seasonality가 변동할 때 승법모형을 이용한 분해가 더 적절함  (즉, seasonality가 non-linear하고, 시간에 따라 변동의 진폭이 더 커지거나 감소할 때)

 

---

 

python에서 이용할 수 있는 함수 

 

statsmodel library에서 제공하는 seasonal_decompose( ) 함수를 이용할 수 있다.

raw 시계열 데이터에 이 함수를 적용하면 

- trend, seasonal, resid(udal), observed 4개에 대한 시간에 따른 값이 array로 출력된다. 

- 여기서 'observed'는 기존의 time series (분해 전)을 의미한다. 

 

from statsmodels.tsa.seasonal import seasonal_decompose

from matplotlib import pyplot

series = ...

result = seasonal_decompose(series, model='additive')

result.plot()

pyplot.show()

 

 

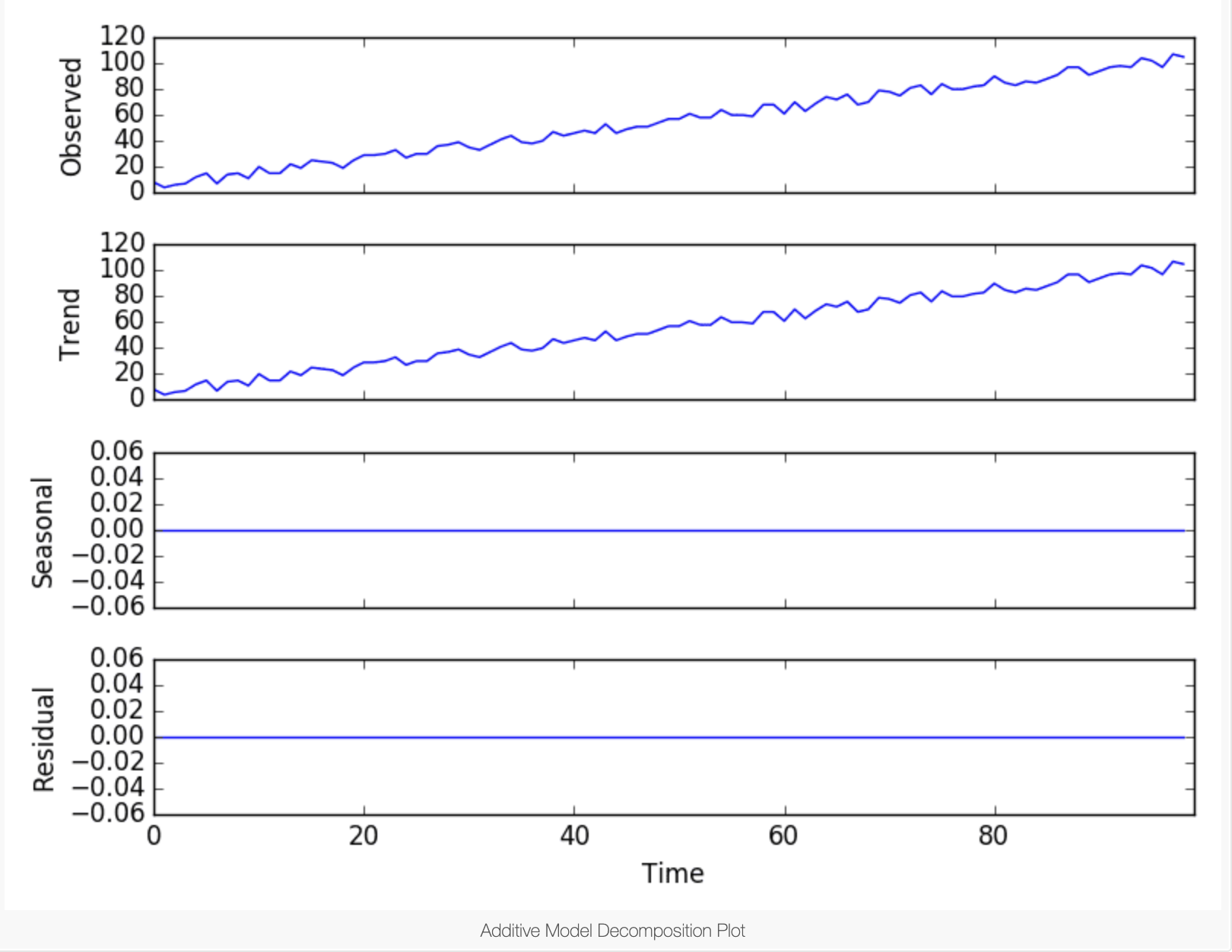
위와 같이 time series에 대하여 model = 'addictive' : 가법 모형을 적용하면 

아래 그림과 같이 분해 결과가 나온다. 

 

해당 케이스의 경우에는 seasonality와 residual이 모두 없는 경우에 해당됨

출처 : https://machinelearningmastery.com/decompose-time-series-data-trend-seasonality/

 

 

from statsmodels.tsa.seasonal import seasonal_decompose

from matplotlib import pyplot

series = ...

result = seasonal_decompose(series, model='multiplicative')

result.plot()

pyplot.show()

 

 

이번에는 가법모형을 적용해야 할 series에 가법모형을 적용하여 분해한 결과를 살펴보자. 

 

출처 : https://machinelearningmastery.com/decompose-time-series-data-trend-seasonality/

 

 

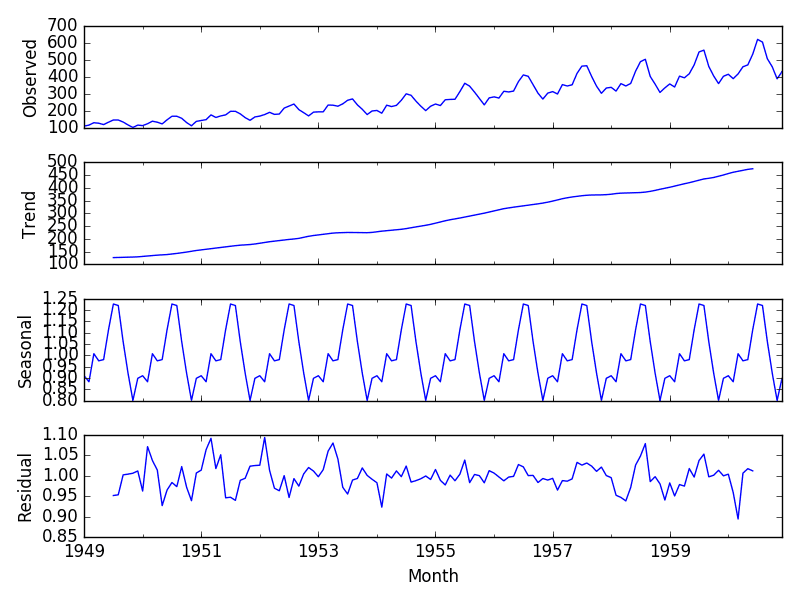
위 결과는 시간에 따른 항공기 탑승객의 수에 대한 시계열 데이터를 분해한 결과이다. 

Observed를 보면 시간이 지남에 따라 1년마다 반복되는 저 모양의 진폭이 더 커짐을 눈으로 확인할 수 있기 때문에 

가법모형을 적용한 것이다. 

 

그 결과 증가하는 trend, 그리고 1년 주기의 seasonality, 설명할 수 없는 오차에 해당하는 residual이 나왔다. 

residual의 경우 마지막 2년에 갑자기 이전과 다르게 급감하는 부분이 존재하는데, 이렇게 seasonality와 trend를 모두 제거한 다음에 보이는 특이한 패턴에 대하서 추가 eda를 해볼 수 있을 것이다.