0. 일단 time series data에 대해 스무딩 (평활) 기법을 적용하려면 계절성을 제거해야 한다.
1. 단순 이동평균 : Simple Moving Average
window 사이즈 = k일때
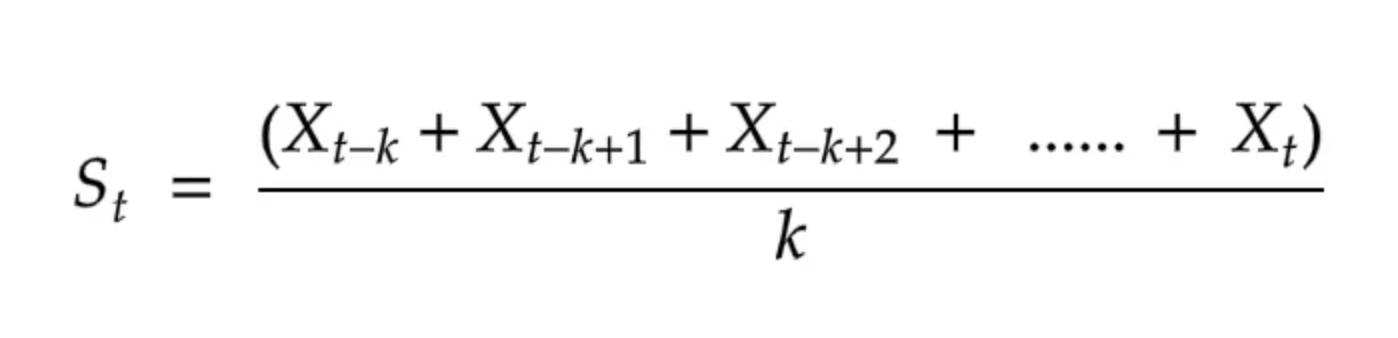
현 시점 포함 k개의 과거 데이터에 대한 평균값을 이용
당연히 window size : k가 커질수록 변동성이 감소하지만 lagging 현상이 발생하고 데이터의 움직임에 대한 섬세함이 떨어진다는 단점이 있다. 순간적인 변화에 대응하는 것이 중요하고, 이에 민감해야 한다면 트레이드 오프를 고려하여 적절한 window size를 정하는 것이 중요할 수 있다.
또, '평균'이라는 통계치가 outlier에 굉장히 취약하게 반응한다는 것이 잘 알려져 있다. 이런 이유로 어떤 경우에는 평균값 대신 median값을 반영하기도 한다고 한다.
2. 지수 이동평균 : Exponential Moving Average
현재 시점에 대한 smoothed value를 산출하기 위해서 과거 데이터에 대해 지수적으로 감소하는 weight를 매기는 방법이다. weight는 smoothing parameter이라고 부르는 alpha값으로 정해진다. (0<alpha<1) alpha값이 높을수록 최근의 관측치에 더 가중치를 많이 주는 것을 의미한다. 단순 이동평균 방법보다 현재 관측값에 더 민감하게 반응한다는 장점이 있다. (추가로, computation도 덜 소요된다고 한다. )
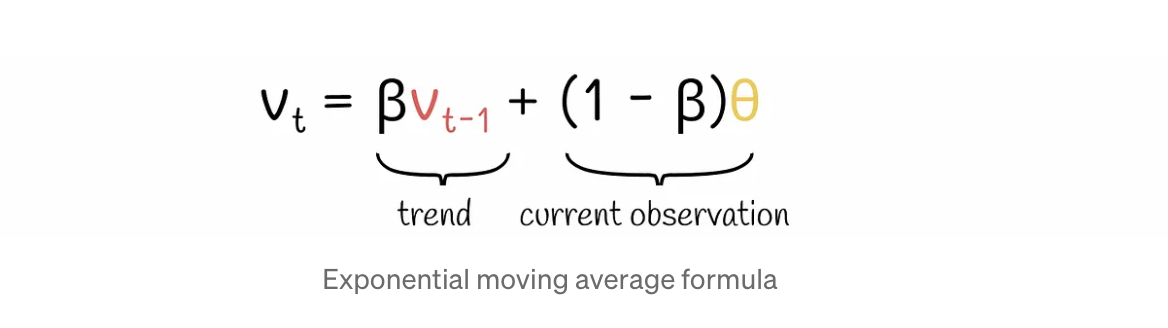
- vₜ 는 현재 시점에 대해 smoothed value를 의미한다.
- θ 는 현재 시점에 대해 smoothed 되기 전의 value를 의미한다.
- β 는 0과 1 사이의 hyperparameter로 현재 관측치 θ와 이전 시점 smoothed value인 vₜ-₁ 사이에 얼마나 가중치를 부여할지를 의미한다.
위 식은 재귀적 수식이므로 정리하면 다음과 같이 정리된다.

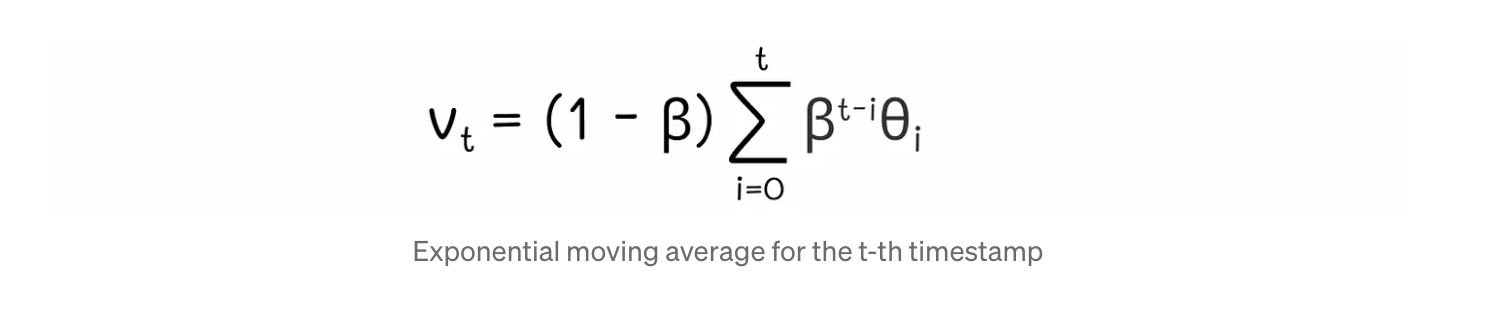
(1-β)는 모든 항에 공통적으로 곱해지는 수치이고 그 외의 weight가 곱해지는 양상을 보면
과거시점으로 갈수록 β값이 추가적으로 곱해져, 가중치가 더 작아짐을 확인할 수 있다.
β = 0.9일때 timestamp별로 곱해지는 가중치는 아래 사진과 같이 지수적으로 감소함을 확인할 수 있다.

윈도우 크기에 따라서 β값이 달라진다.
k-day EMA를 구할 때 1-β = 2/(k+1)이다. 예를 들어 4일 윈도우의 지수 이동평균을 적용하고자 할 때는 1-β = 0.4 (β=0.6)을 적용하면 된다.
윈도우 크기 k가 커질수록 β값이 커지고 이는 최근의 값에 비해 과거 시점의 값에 대한 가중치가 더욱 급격하게 감소할 것임을 의미한다.
3. Savitzky-Golay filter
정해진 윈도우 사이즈에 대해서 윈도우를 슬라이딩하면서 해당 구간에 대해 다항 회귀함수를 적용하여 구간의 중간 시점에 대핸 smoothed value를 구하는 방식이다. 관측값과 예측값(smoothed value) 사이의 error의 제곱 합을 최소화하는 방식으로 회귀된다.
시계열 데이터가 원래 시간에 따라는 변하는 양상을 최대한 잘 보존하면서도 노이즈나 이상치를 최대한 줄이는 효과를 보인다.
하지만 이렇게 다항회귀함수를 매 구간마다 계산해줘야 한다는 것이 매우 비효율적으로 보일 수 있다.
따라서 Savitzky-Golay filter(S-G filter)는 회귀모델을 이용한 smoothing을 수행함에 있어
매 time step 구간마다 회귀함수를 계산하지 않고도 특정한 impulse response를 통해 수학적으로 다항회귀함수를 이용한 smoothing을 대체할 수 있는 개념이다. 즉, 적절히 계산된 impulse response를 이용하여 매 구간마다 회귀모델을 계산하는 것과 같은 효과를 얻을 수 있도록 만든 필터라는 것이다.
(impulse response에 대한 요약 개념 / s-g filter 개념 출처 : https://angeloyeo.github.io/2020/10/21/Savitzky_Golay.html)
'Study > 머신러닝' 카테고리의 다른 글
| 시계열 분해 (2) | 2024.07.22 |
|---|---|
| WandB 사용법 (0) | 2024.03.02 |
| 차원 축소 (0) | 2023.10.29 |
| 앙상블 학습 - Bagging (0) | 2023.09.25 |
| Decision Tree : 가지치기 (pruning)에 대하여 (1) | 2023.09.15 |
